Logistic Regression

Linear regression could not yield proper result in classification Problem, because outliers could affect the result.

Logistic Regression is still a classification algorithm, even though it is called regression.

Hypothesis Function

Logistic regression uses the “Sigmoid Function” (or “Logistic Function”) as hypothesis function:

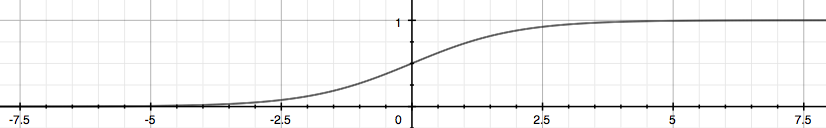
Logistic Function

h_\theta(x)=g(\theta^T x)
g(z) = \frac{1}{1 + e^{-z}}

h_\theta will give us the probability that our output is 1.

h_\theta(x) = P(y=1 | x ; \theta) = 1 - P(y=0 | x ; \theta)

Decision Boundary

Decision boundary is on h_\theta(x) = 0.5 , also \theta^Tx = 0
It is a feature of the trained model (parameters).

Non linear decision boundaries:
Just create new features to fit.

Cost Function

$
J(\theta) = \frac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)})


\begin{eqnarray} Cost(h_\theta(x),y) = \begin{cases} -\log(h_\theta(x)) & \text{if }y=1 \ -\log(1-h_\theta(x)) & \text{if }y = 0 \end{cases} =-y\log(h_\theta(x)) - (1 - y)\log(1 - h_\theta(x)) \end{eqnarray}
$

Vectorized version:

J(\theta) = -\frac{1}{m}(\log(g(X\theta))^{T}y+\log(1-g(X\theta))^{T}(1-y))

Why not Using Squared Error？

If using squared error on sigmoid function, it will be non-convex, so that we can’t use gradient descent.

Optimization

Derivative for Gradient Descent

It looks identical to linear regression
$
\frac{d}{d\theta_j}J(\theta)=\frac{1}{m}\displaystyle\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j}

$

$
J(\theta_0,\theta_1,\theta_2, …) = \frac{1}{m}\displaystyle\sum_{i=1}^m{Cost(h_\theta(x^{(i)}), y^{(i)})}+\frac{\lambda}{2m}\displaystyle\sum_{j=1}^n{\theta^2_j}

$

( \lambda is regularization parameter)

Update \theta :
$
\theta_j = \theta_j -\frac{\alpha}{m}\displaystyle\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j}

$
Vectorized implementation:

\theta = \theta - \frac{\alpha}{m} X^{T} (g(X \theta ) - y)